Ajustement de données, du questionnement à l'écriture du code

            Depuis la semaine dernière, nous nous sommes rencontrés deux fois. Durant la première rencontre, nous avons travaillé sur la bonne méthode à adopter, sur le plan général de notre programme sur Python. La deuxième a été consacrée a la mise « en code » de notre plan.

1-Le plan

En partant d’une liste de valeurs yi, qui sont censés être approchés par une fonction sinusoïdale, comment le programme python va-t-il donner les valeurs les plus justes en se servant de la méthode des moindres carrés aux quatre paramètres de cette fonction?

h(t) = A.sin(wt + f) + B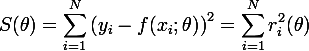                                 

Nous avons choisis la dichotomie. On s’explique: on fixe trois variables, on fais changer la quatrieme d'un certain pas définit "à l'avance" (nous lui ajoutons ou retranchons ce pas). Si S diminue, on sauvegarde la nouvelle valeur de cette variable, si S augmente, nous divisons ce pas par deux pour refaire ulterieurement la meme opération (car il faut appliquer ce procédé aux autres variables).

D'accord, mais quel pas choisir?

Il  faut un pas de départ adapté pour chaque variable de la fonction h(t). Apres quelques tractations, notre choix s'est porté sur les pas de depart suivants:

rappelons nos valeurs de départ des quatre variables:

A = Ymax – Ymin

            Ymax : valeur maximale de « yi »

            Ymin : valeur minimale de « yi »

B = (Ymax + Ymin)/2

w = 1

f = 0

P(B): la difference entre l'ordonnée du premier point de notre échantillon avec la moyenne B du plus grand et du plus petit des points de l'échantillon. P(B)= | y1 - B |

P(A): soit Ym la moyenne générale de tous les points de l'échantillon: Ym= (y1+y2+...+yn)/n. P(A)= | Ym - A |

P(f): soit Xmax et Xmin les abscisses des points maximal et minimal de l'échantillon. P(f)= ( | Xmax - Xmin | ) / 2 

P(w): un taux d'accroissement approximatif, soit P(w)= (Ymax - B) / Xmax

Deuxième question: Jusqu'ou aller? Notre professeur (orienté physique) nous dit que l'on peut remplir toute une bibliothèque des livres qui ont été écrits sur l'approximation de fonction, et entre autre, sur le critère qui fait dire "Stop! Ça suffit, nous avons la meilleure fonction..."

Etant très limité dans la puissance de calcul (la preuve en a été faite lors du l'approximation de la valeur de pi avec notre professeur orienté informatique), nous avons jugé bon de rajouter un paramètre a notre programme Python que l'on va noter P et qui déterminera le nombre d'itérations du procédé dichotomique. Ce paramètre va nous permettre de disposer d'une échelle de "précision" et d'un critère d'arrêt fixé à l’ avance, ce qui va empêcher toute boucle infinie.

Récapitulons:  

Notre Programme Python prends comme arguments une liste l et une valeur P, il nous retourne une fonction sinusoïdale et le tracé de sa courbe.

Nous avons besoin:

De savoir déterminer, en Python, la valeur maximale et minimale d'une liste et donner les abscisses de ces deux points (ou la valeur prise par n) pour avoir nos: Ymax, Ymin, Ym, Xmax, Xmin. Avec ceux-là nous avons les valeurs initiales et les pas pour chaque variable.

D'une fonction "erreur" ou S(B,A,w,f) qui va calculer le reste par les moindres carrés en fonctions des quatre paramètres que nous aurons a changer lors du procédé par dichotomie pour affiner notre courbe.

D'une code en python efficace pour pouvoir ajouter ou retrancher le pas a une variable jusqu'a ce que cette opération ne réduise plus l'erreur, dans ce cas, diviser le pas en deux, passer aux autres variable (qui ont un pas diffèrent),sauvegarder a chaque fois la meilleure valeur pour chaque variable, faire la même opération P fois.

De savoir retourner la courbe sinusoïdale de la fonction obtenue.

2-Le code

(l est la liste des ordonnée, v est la liste des abcisses), nous n'avons pas inclus le tracé de la courbe finale et des points provenants des données experimentales)

import matplotlib.pyplot as plt

largeur= len(l)


def absmax (l):
Xmax=0
Ymax=max(l)
while l[i]<Ymax:
Xmax= Xmax+1
Xmax= v[Xmax]
return Xmax,Ymax

def absmin (l):
Xmin=0
Ymin=min(l)
while l[i]>Ymin:
Xmin= Xmin+1
Xmin= v[Xmin]
return Xmin,Ymin


def Somme(B,A,w,f):
u = 0
i = 0
for i in range(0,largeur):
u = (l[i]-(B + A *sin(wt + f))) ** + u
return u




def moindrecarre(l,P):
A =Ymax-Ymin
B =(Ymax+Ymin)/2
w = 1
f = 0

for i in range(0,P):

ajustement= Somme(B,A,w,f)

plusB= Somme(B+PB,A,w,f)
moinsB=Somme(B-PB,A,w,f)

plusA= Somme(B,A+PA,w,f)
moinsA=Somme(B,A+PA,w,f)

plusw= Somme(B,A,w+Pw,f)
moinsw=Somme(B,A,w+Pw,f)

plusf= Somme(B,A,w,f+Pf)
moinsf=Somme(B,A,w,f+Pf)

if plusB<ajustement:
while plusB<ajustement:
B=B+PB

elif moinsB<ajustement:
while moinsB<ajustement:
B=B-PB
else:
PB=PB/2
if plusA<ajustement:
while plusA<ajustement:
A=A+PA
elif moinsA<ajustement:
while moinsA<ajustement:
A=A-PA
else:
PA=PA/2
if plusw<ajustement:
while plusw<ajustement:
w=w+Pw
elif moinsw<ajustement:
while moinsw<ajustement:
w=w-Pw
else:
Pw=Pw/2
if plusf<ajustement:
while plusf<ajustement:
f=f+Pf
elif moinsf<ajustement:
while moinsf<ajustement:
f=f-Pf
else:
Pf=Pf/2
return B,A, w,f